[Algorithm] 최대공약수, 최소공배수

1. 최대공약수(Greatest Common Divisor)

유클리드 호제법 은 두 자연수 A, B (단, A>B)의 최대공약수를 구하는 방법으로 아래 2가지 사실을 활용한 알고리즘이다.

• gcd(A,B) == gcd(B, R) (R은 A%B)
• R 이 0 이면 B가 최대공약수

재귀법 또는 반복문으로 코드를 작성할 수 있다.

• 재귀법

  fun gcd(a: Int, b: Int) {
    if (b == 0) return a
    return gcd(b, a % b)
  }
  

• 반복문

  fun gcd(a: Int, b: Int) {
    var r = 0
    while (b > 0) {
        r = a % b
        a = b
        b = r
    }
    return a
  }
  

2. 최소공배수(Least Common Multiple)

A와 B의 최소공배수는 gcd * (A/gcd) * (B/gcd) 공식으로 구할 수 있다. 아래 그림을 보면, 최소공배수를 구하는 방법이 잘 연상될 것이다.

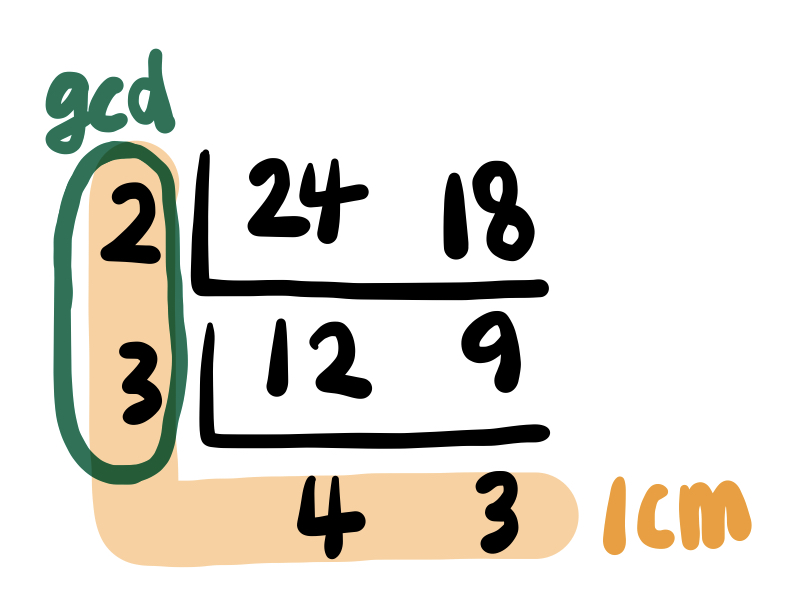
24를 A라고 할 때, A/gcd는 4이다.

fun lcm(a: Int, b: Int) : Int {
    return a * b / gcd(a,b)
}